Optimal Algorithms for Statistical Inference and Learning under Information Constraints
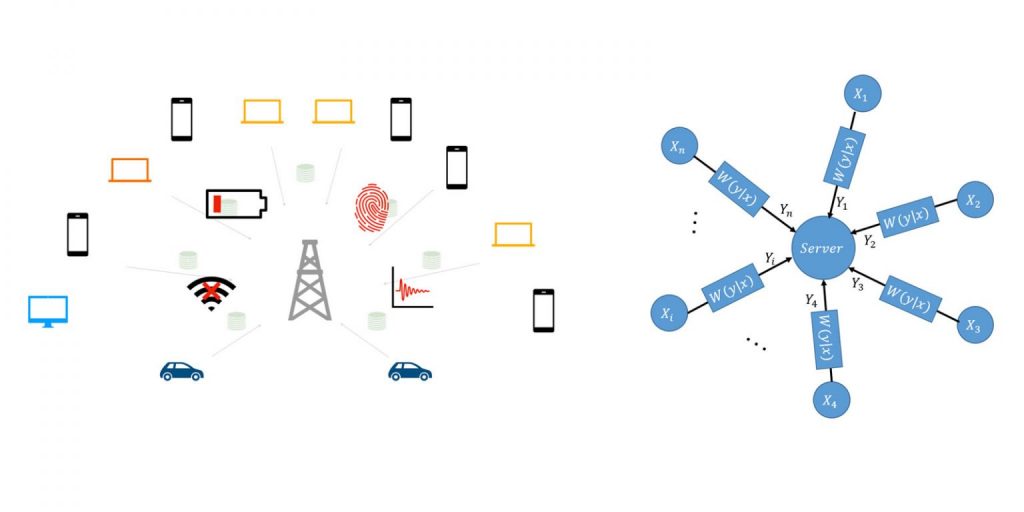
Classical statistics assumes that data samples are available in their entirety at one place. But what happens when only limited information is allowed about each sample from a user? The information can be constrained in form of communication constraints as in federated learning or local privacy constraints. We have developed a general framework for design and analysis of statistical and optimization procedures under such distributed information constraints.
References:
J Acharya, C Canonne, and H Tyagi, “Inference under information constraints: Lower Bounds from Chi-Square Contraction,” Proceedings of the Thirty-Second Conference on Learning Theory (COLT), PMLR 99:3-17, 2019.
P Mayekar and H Tyagi, “RATQ: A Universal Fixed-Length Quantizer for Stochastic Optimization” Proceedings of the Twenty Third International Conference on Artificial Intelligence and Statistics (AISTATS), PMLR 108:1399-1409, 2020.
Website: https://ece.iisc.ac.in/~htyagi/
Faculty: Himanshu Tyagi, ECE